牛吃草問題，是行測中比較常見的一類題型，在這類題型中最常考的兩類題型是追及型牛吃草和相遇型牛吃草，只要掌握這類題型的做題原理和方法，就能快速準確地選出正確答案。今天分享這兩類題型的原理和方法。
一、追及型牛吃草
例1.一片草地上草每天都均勻地生長，如果放24頭牛，則6天吃完牧草;如果放21頭牛，則8天吃完牧草。問如果放16頭牛，幾天可以吃完牧草?
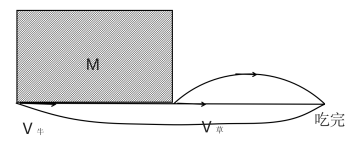
如圖所示，用M表示草地上的原始草量，牛吃草使草量減少，草在勻速生長使草量增加，牛吃完草的時候相當于牛追上了正在生長的草，構成了一個追及問題，而原始草量M就是牛比草多走的路程。我們假設每頭牛單位吃草量為1，草單位時間生長量為x，設16頭牛t天可以吃完，則原始草量M=(24-x)×6=(21-x)×8=(16-x)×t，解得x=12，t=18，所以16頭牛18天可以吃完牧草。
根據這道題，我們可以得出追及型牛吃草的做題公式，假設每頭牛單位吃草量為1，草單位時間生長量為x，牛吃草的時間記為T，則原始草量M=(牛的數量-x)×T。
二、相遇型牛吃草
例2.一片草地上草每天都勻速枯萎，如果放2頭牛，7天可以吃完;如果放3頭牛，6天可以吃完。若要在3天內吃完，則需要多少頭牛?
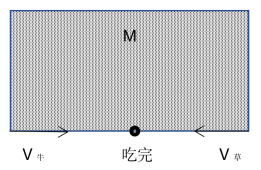
如圖所示，我們依然用M表示草地上的原始草量，牛吃草使草量減少，草在勻速枯萎也使草量減少，牛吃完草的時候相當于牛與正在枯萎的草相遇了，構成了一個相遇問題，而原始草量M就是牛與草走的路程和。假設每頭牛單位吃草量為1，草單位時間枯萎量為x，設y頭牛3天可以吃完，則原始草量M=(2+x)×7=(3+x)×6=(y+x)×3，解得x=4，y=10，所以10頭牛3天可以吃完牧草。
根據這道題，我們可以得出相遇型牛吃草的做題公式，假設每頭牛單位吃草量為1，草單位時間枯萎量為x，牛吃草的時間記為T，則原始草量M=(牛的數量+x)×T。
綜上所述，可以總結，追及型牛吃草是牛吃草使草量減少、草生長使草量增加的題型;相遇型牛吃草是牛吃草使草量減少、草枯萎也使草量減少的題型，做題時分析清楚這兩個因素使原始草量增加還是減少從而確定用哪個公式做題即可。
新公教育為你提供更多考試資訊和招聘公告可關注微信公眾號【新公教育（cqxgjy）】查看！
公職類、事業單位考試培訓 全國 電話：023-65009134
咨詢電話：023-65009134 真題 講義：023-65009134
地址：沙坪壩東原ARC中央廣場1棟20F(石碾盤88號) 023-65009134
重慶新公教育、國家公務員考試、重慶事業單位招聘考試、重慶教師招聘考試
網址： http://www.k0800.com Email： 290845968@QQ.com
渝公網安備 50010602502030號
