新公微信公眾號【新公教育】(cqxgjy) | 備考QQ群:810828910 | 備考課程:一年/兩年協議無限學
———————————————————————————————————
容斥問題在你眼中是否繁瑣呢?采用容斥問題的公式或者借助文氏圖分析,相信雙通道可幫助同學們繞出容與斥的復雜;極值問題是否也帶給你困擾?常見和定求最值、為保證完成目的的最不利分析、行走最短路程的探索等,協助了同學們一點點熟知極值的脾性。而容斥問題與極值問題共同孕育的容斥極值,讓多集合在全集中使勁擠兌,數量關系與資料分析的考查中,它皆是常客。很多同學感覺它走出了繁瑣與困擾,有些負負得正的韻味。如何分析應用呢?
例題1:在陽光明媚的一天下午,甲乙兩人給30盆花澆水,已知甲澆了20盆花,乙澆了17盆花。假設甲乙兩人給每盆花澆水量相同,且每盆花澆水不宜過量,若重復澆水需放到室外光照、風量較好處養護,那么兩人澆水后至少搬至室外多少盆花?
A.3 B.5 C.7 D.9
【解析】正確答案為C。共有30盆花,甲澆了20盆花,乙澆了17盆花,所以必會存在兩人均澆過的花,即重復澆水需移至室外養活的花。根據兩者容斥問題的公式:I=A+B-A∩B+M,即30=20+17-A∩B+M,得A∩B=7+M。若要A∩B最小,那么M的值也要盡可能小,M最小可取0,此時A∩B最小為7,故本題選C。(注:I表示全集,A、B分別表示全集中的兩個集合,M表示既不屬于集合A也不屬于集合B的部分,即補集)
在花朵都如此有求生欲的今天,這一題在考場上又怎會不寶貴呢?但經過分析可知此題的計算難度并不高,所求為兩集合公共部分的最小值,即在全集中既不屬于A集合也不屬于B集合的M取得0的前提下求得(A∩B)min=A+B-I。以此類推,若在容斥中求極值,則全集中多集合間公共部分的最小值分為:
(A∩B)min=A+B-I;
(A∩B∩C)min=A+B+C-2I
(A∩B∩C∩D)min=A+B+C+D-3I
……
例題2:2019年年末全國大陸總人口140005萬人,比上年末增加467萬人,其中,城鎮常住人口84843萬人,占總人口比重(常住人口城鎮化率)為60.60%,比上年末提高1.02個百分點。戶籍人口城鎮化率為44.38%,比上年末提高1.01個百分點。全國人戶分離的人口占大陸總人口的20%,其中,84.29%為流動人口。
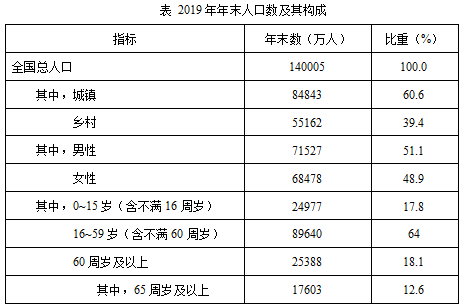
問題:2019年年末,城鎮常住人口中,男性人口占比至少為:
A.5.2% B.11.7% C.17.5% D.19.3%
【解析】正確答案為D。所求為城鎮常住人口中的男性人口占比,由表格可知,2019年年末,城鎮常住人口占全國總人口比重為60.6%,男性人口占全國總人口比重為51.1%,則既是城鎮常住人口又是男性人口占總人口的比重至少為60.6%+51.1%-1=11.7%,則城鎮常住人口中,男性人口至少占11.7%÷60.6%≈19.3%,選擇D項。
容斥極值求解可還容易判定?即求解多個集合公共部分的極值,在數量關系與資料分析的考查中均可現影,看似復雜其實多加訓練后,你會對它由陌生到熟悉,好感慢慢升級。所以夯實容斥問題的基底,練就推導本領,即使難題亦可迎刃而解,希望同學們在訓練中都可有更大收獲!
新公教育為你提供更多考試資訊和招聘公告可關注微信公眾號【新公教育(cqxgjy)】查看!
